dot product (scalar product)

Apa itu dot product (perkalian skalar)?

Dot product, atau disebut juga perkalian skalar, adalah cara untuk mengukur seberapa sejajar atau searah dua vektor. Hasil pengukurannya berupa sebuah nilai skalar (satu angka) yang bisa dipakai untuk membandingkan dua vektor dan melihat bagaimana efek perubahan posisi salah satunya atau keduanya. Nilai dot product didapatkan lewat perhitungan matematis berdasarkan properti vektor.

Vektor sendiri adalah besaran yang punya arah sekaligus magnitudo (panjang vektor). Gambar 1 menunjukkan dua vektor (a dan b) pada bidang Cartesius 2D. Vektor a memiliki magnitudo 8 dan membentuk sudut 115° dari sumbu x (berlawanan arah jarum jam). Vektor b punya magnitudo 10 dan membentuk sudut 45° dari sumbu x. Sudut antara kedua vektor — dilambangkan dengan huruf Yunani theta (θ) — adalah 70°, hasil pengurangan 115° dengan 45°.

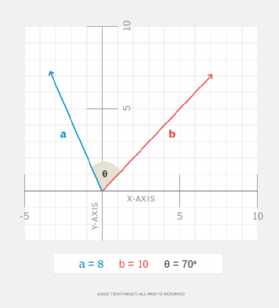
Jika magnitudo dua vektor dan sudut di antara keduanya diketahui, menghitung dot product jadi mudah. Notasinya menggunakan tanda titik di antara dua vektor, misalnya a dan b, seperti pada rumus berikut:

a • b

Rumus lengkap untuk dot product adalah dengan mengalikan magnitudo vektor a dengan magnitudo vektor b, lalu mengalikan hasilnya dengan cosinus (cos) sudut di antara kedua vektor:

a • b = |a| × |b| × cos(θ)

Simbol garis tegak di kiri dan kanan melambangkan magnitudo vektor. Kadang dipakai garis ganda untuk notasi yang sama. Jika nilai pada Gambar 1 dimasukkan, perhitungannya jadi:

a • b = 8 × 10 × cos(70°)
a • b = 8 × 10 × 0.342
a • b = 27.36

Nilai cos dari 70° dibulatkan ke tiga angka desimal, jadi hasil akhirnya (27.36) adalah pendekatan, meskipun cukup akurat.

Kalau magnitudo dan sudut tidak diketahui, dot product bisa dihitung pakai rumus komponen:

a • b = (a_x × b_x) + (a_y × b_y)

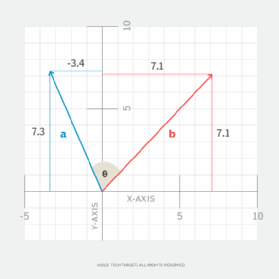
Dalam hal ini, komponen vektor dipecah ke arah sumbu x dan y pada bidang Cartesius. Dari Gambar 2:

Vektor a = (-3.4, 7.3)

Vektor b = (7.1, 7.1)

Rumusnya menjadi:

a • b = (a_x × b_x) + (a_y × b_y)
a • b = (-3.4 × 7.1) + (7.3 × 7.1)
a • b = -24.12 + 51.83
a • b = 27.71

Karena ada pembulatan, hasil (27.71) sedikit berbeda dari perhitungan sebelumnya (27.36), tapi keduanya menunjukkan metode ini valid.

Pendekatan serupa berlaku untuk ruang 3 dimensi dengan menambahkan komponen z:

a • b = (a_x × b_x) + (a_y × b_y) + (a_z × b_z)

Misalnya, jika a_z = b_z = 5, maka:

a • b = (-3.4 × 7.1) + (7.3 × 7.1) + (5 × 5)
a • b = -24.12 + 51.83 + 25
a • b = 52.71

Hasilnya 25 lebih besar dari 27.71 sebelumnya karena ada tambahan dari komponen z.

Dot product sering digunakan di fisika, matematika, dan bidang lain yang aplikatif. Contoh praktisnya adalah pada pemasangan panel surya. Dengan membandingkan sudut datang cahaya matahari dengan sudut panel, insinyur bisa menghitung posisi terbaik untuk memaksimalkan energi yang diserap sepanjang hari.

Lihat juga: Simbol matematika